40-双因素方差分析(有交互):原理、SPSS应用、结果解读、结论撰写

 、
、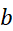 两个因素对因变量影响的
两个因素对因变量影响的 ×
× 析因设计,因素
析因设计,因素 有
有 个水平,因素
个水平,因素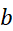 有
有 个水平,研究对象被分为
个水平,研究对象被分为 ×
× 个组。采用双因素方差分析不但可以解释因素
个组。采用双因素方差分析不但可以解释因素 和因素
和因素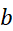 单独对因变量的影响,还可以探索因素
单独对因变量的影响,还可以探索因素 与因素
与因素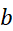 的最佳水平组合,以及两者的相互影响或调节效应。
的最佳水平组合,以及两者的相互影响或调节效应。|
例7-3-2 为探索不同锻炼方法对肥胖初中生减肥效果的影响,筛选了12名(6男、6女)满足条件的受试者,男生和女生分别随机分为2组(HIIT组、持续有氧组)。实验前测试2组受试者的体脂率(前测),经检验,组间差异不具有统计学意义。然后分别进行了6个月的HIIT训练和持续有氧训练,实验结束后再次测试体脂率(后测)。体脂率的前测与后测差值作为减肥效果的评价指标,用“D_BFP”表示。数据集:7_03.sav。 注:本例仅用于介绍统计方法,大家可以忽略样本量不足的问题。 |
与例7-3-1同样的研究设计,但数据集替换为“7_03.sav”,采用与上文同样的SPSS操作(39-双因素方差分析(无交互):原理、SPSS应用、结果解读、结论撰写),得到的主要结果如下。
1.主效应、交互效应分析
(1)描述性统计表
表7-5-9给出了描述性统计结果,包括各组的均值、标准差、个案数。
表7-5-9 描述性统计表

(2)方差分析表
据表7-5-10,训练方法与性别的交互效应具有统计学意义,=245.841,<0.05,偏 =0.968>0.138;训练方法的主效应具有统计学意义,=28.571,<0.05,偏
=0.968>0.138;训练方法的主效应具有统计学意义,=28.571,<0.05,偏 =0.781>0.138;性别的主效应具有统计学意义,=6.222,<0.05,偏
=0.781>0.138;性别的主效应具有统计学意义,=6.222,<0.05,偏 =0.438>0.138。
=0.438>0.138。
表7-5-10 主体间效应检验结果表

(3)多重折线图
“D_BFP”的多重折线图(图7-5-7)显示,两条线明显交叉。线或其延长线的明显交叉是交互效应在图形中的表现形式。

图7-5-7 “D_BFP”的多重折线图
(4)交互效应显著时结果的解释
交互效应显著时,需要先解释交互效应,再解释主效应,主效应往往只起到参考作用。比如在本例中,对任何主效应的解释都没有实际意义。根据表7-5-5所示锻炼方法的主效应具有统计学意义,如果做出推断结论“HIIT的减肥效果比持续有氧好”,那么考虑“性别”因素后会发现这一结论显然是不正确的。因为据图7-5-7所示,对于“男生”,HIIT组的“D_BFP”均值小于持续有氧组,此时HIIT的减肥效果不可能比持续有氧好;对于“女生”,HIIT组的“D_BFP”均值大于持续有氧组,此时HIIT的减肥效果有可能比持续有氧好。前面的推断之所以用“不可能”和“可能”,是因为本例没有在固定“性别”取值时对“锻炼方法”进行组间差异性检验。这种检验就是下面要介绍的简单效应分析。在某些特殊情况下,交互效应显著时,主效应也会具有一定的实际意义,比如在本例中如果图7-5-7左侧的两个均值都小于右侧的两个均值,且两条线有明显的交叉(交互效应显著),那么“性别”的主效应就可能具有一定的实际意义;如果图7-5-7中HIIT组的两个均值都高于持续有氧组,且两条线的延长线有明显的交叉(交互效应显著),那么“锻炼方法”的主效应就可能具有一定的实际意义。读者朋友们可以把本例的数据集替换为“7_04.sav”试一试。
2.简单效应分析
交互效应显著时,还需要分析简单效应,用于探索自变量间的相互影响或调节情况。也就是固定一个自变量的水平值,分析另一个自变量对因变量的影响。这需要在原有SPSS操作的基础上借助语法完成。
-
1.操作步骤
(1)在“单变量”对话框(图7-5-2)中点击“EM平均值”,打开“估计边际平均值”对话框(图7-5-8)。点击“继续”,返回主对话框。

图7-5-8 “估计边际平均值”对话框
(2)在主对话框点击“粘贴”,打开“语法”窗口。把“EMMEANS”语句修改为:
/EMMEANS=TABLES(训练方法*性别) COMPARE(训练方法)ADJ(LSD)
/EMMEANS=TABLES(训练方法*性别) COMPARE(性别)ADJ(LSD)
第一句用于固定“性别”的取值,分析不同训练方法的差异;第二句用于固定“训练方法”的取值,分析不同性别的差异。“语法”窗口见图7-5-9。

图7-5-9 “语法”窗口
(3)选择所有语句,点击图7-5-9中的“运行选定项”按钮 ,查看结果。
,查看结果。
-
2.基于估计边际均值的结果
(1)描述性统计结果的估算值表
表7-5-11给出了“D_BFP”的估算值(边际均值),包括平均值、标准误、95%置信区间。
表7-5-11 描述性统计结果的估算值

(2)固定“性别”时的简单效应分析结果
表7-5-12给出了固定“性别”时采用LSD法的两两比较结果,具体包括对比的组别I和J、均值差(I-J)、均值差的标准误、 值、均值差的95%置信区间。
值、均值差的95%置信区间。
无论是男生组还是女生组,持续有氧组与HIIT组的差异都具有统计学意义( <0.05)。结合均值差可知,对于男生,持续有氧组的“D_BFP”显著高于HIIT组;但是对于女生则相反。
<0.05)。结合均值差可知,对于男生,持续有氧组的“D_BFP”显著高于HIIT组;但是对于女生则相反。
表7-5-12 成对比较结果

表7-5-13给出了单变量检验(单因素方差分析)结果,具体包括固定“性别”时组间对比的平方和、自由度、均方、 、
、 、偏
、偏 、非中心参数、实际幂。对于男生组,
、非中心参数、实际幂。对于男生组, <0.05,偏
<0.05,偏 =0.870>0.138;对于女生组,
=0.870>0.138;对于女生组, <0.05,偏
<0.05,偏 =0.965>0.138。与表7-5-12呈现的结果基本一致。
=0.965>0.138。与表7-5-12呈现的结果基本一致。
表7-5-13 单变量检验结果

(3)固定“训练方法”时的简单效应分析结果
表7-5-14给出了固定“训练方法”时采用LSD法的成对比较结果。
无论是持续有氧组还是HIIT组,男生与女生的差异都具有统计学意义( <0.05)。结合均值差可知,对于持续有氧组,男生的“D_BFP”显著高于HIIT组;但是对于HIIT组则相反。
<0.05)。结合均值差可知,对于持续有氧组,男生的“D_BFP”显著高于HIIT组;但是对于HIIT组则相反。
表7-5-14 成对比较结果

表7-5-15给出了单变量检验(单因素方差分析)结果。对于持续有氧组, <0.05,偏
<0.05,偏 =0.916;对于HIIT组,
=0.916;对于HIIT组, <0.05,偏
<0.05,偏 =0.954。与表7-5-14呈现的结果基本一致。
=0.954。与表7-5-14呈现的结果基本一致。
表7-5-15 单变量检验结果

交互效应显著,几个简单效应也显著,结合轮廓图(或各处理的边际均值)可以为本例做出推断结论:男生更加适合的减肥锻炼方法是持续有氧锻炼,女生则是HIIT。
